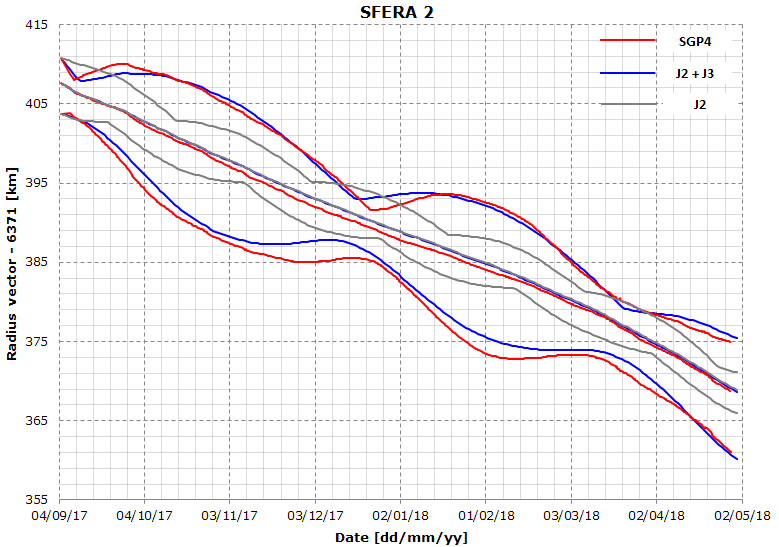
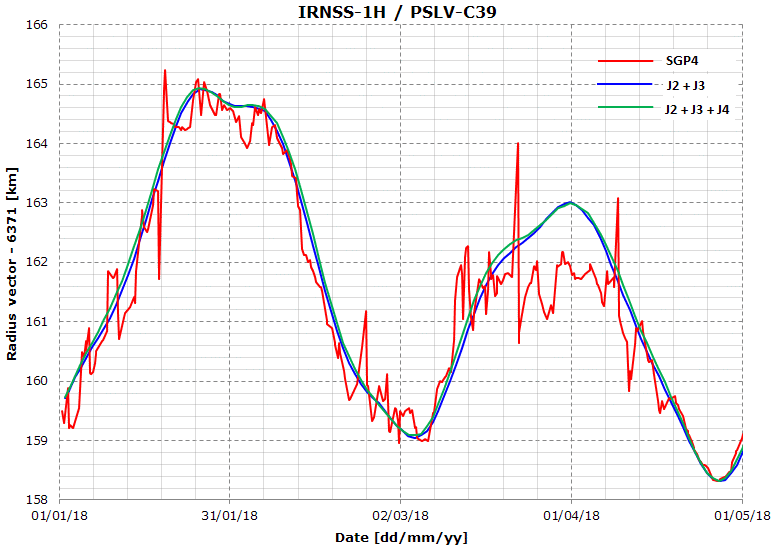
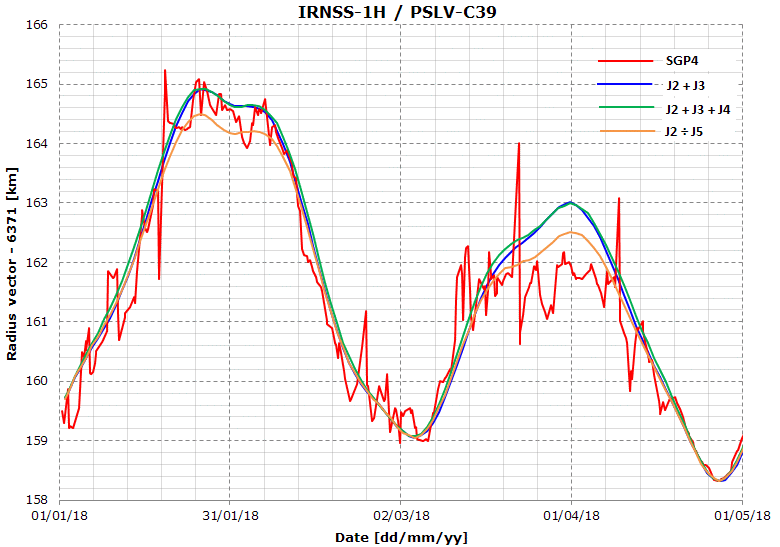
n my simulation, I’m currently using J2 + J3 perturbations (Fx, Fy, Fz) as depicted on this page:
https://en.wikipedia.org/wiki/Geopot...geneous_sphere
but I would also add J4 and possibly J5 too.
Unfortunately, I don’t know how to go from u= J2 * P2(sin theta) / r3 to Fx, Fy, Fz. Please, could anyone explain?
cristiapi:
The wikipedia article that you referenced (
Geopotential model) contains the following expression for the Earth's gravitational potential:
[math]u = -\frac{\mu}{r} + \sum_{n=2}^{N}\frac{J_n\,P_n(\sin\theta)}{r^{n+1}}+\dots[/math]
where [imath]\sin\theta = z/r[/imath] and [imath]r^2 = x^2 + y^2 + z^2[/imath]. All of the [imath]J_n[/imath] are just constants and the [imath]P_n(\xi)[/imath] are just the Legendre polynomials (
Legendre polynomials).
The first term in this expression is the one that gives rise to the usual inverse square law for gravity. The terms involving the [imath]J_n[/imath] are the 'zonal' terms of the expansion. There are other 'tesseral' terms, but we can gloss over these. The first 'zonal' term is, as you point out:
[math]\Delta u_2 = \frac{J_2\,P_2(z/r)}{r^3}[/math]
where, again, [imath]r[/imath] is a function of the [imath]x[/imath], [imath]y[/imath] and [imath]z[/imath] Earth-centred equatorial coordinates. From this contribution to the Earth's gravitational potential we can calculate the corresponding contribution to the gravitational acceleration by substituting [imath]r\to\sqrt{x^2 + y^2 + z^2}[/imath] calculating:
[math]\begin{aligned}
\Delta F_{2,x} &= -\frac{\partial \,\Delta u_2}{\partial x} \\
\Delta F_{2,y} &= -\frac{\partial \,\Delta u_2}{\partial y} \\
\Delta F_{2,z} &= -\frac{\partial \,\Delta u_2}{\partial z}
\end{aligned}[/math]
Let's take the x-component of the force, [imath]F_{2,x}[/imath]. If we take the derivative with respect to [imath]x[/imath], we calculate:
[math]\begin{aligned}
\Delta F_{2,x} &= -J_2\,\frac{3\, x\,\left(x^2+y^2-4\, z^2\right)}{2\, r^7} \\
\Delta F_{2,y} &= -J_2\,\frac{3 \,y\,\left(x^2+y^2-4 \,z^2\right)}{2 \,r^7} \\
\Delta F_{2,z} &= +J_2\,\frac{3 \,z\,\left(-3 \,x^2-3 \,y^2+2 \,z^2\right)}{2\, r^7}
\end{aligned}[/math]
In the same way, we can examine the contribution to the gravitational acceleration arising from the next zonal term
[math]\Delta u_3 = \frac{J_3\,P_3(z/r)}{r^4}[/math]
Again, we refer to the Legendre polynomials tabulated in
Legendre polynomials, make the substitutions [imath]\sin\theta = z/r[/imath] and [imath]r^2 = x^2 + y^2 + z^2[/imath], and finally take the derivatives with respect to [imath]x[/imath], [imath]y[/imath] and [imath]z[/imath]. Then we calculate that:
[math]\begin{aligned}
\Delta F_{3,x} &= -\frac{\partial \,\Delta u_3}{\partial x} = -J_3\,\frac{5 \,x\, z \left(3 \,x^2+3 \,y^2-4 \,z^2\right)}{2 \,r^9} \\
\Delta F_{3,y} &= -\frac{\partial \,\Delta u_3}{\partial y} = -J_3\,\frac{5 \,y\, z \left(3\, x^2+3 \,y^2-4 \,z^2\right)}{2 \,r^9} \\
\Delta F_{3,z} &= -\frac{\partial \,\Delta u_3}{\partial z} = +J_3\,\frac{3 \,x^4+6\, x^2 \left(y^2-4\, z^2\right)+3 \,y^4-24 \,y^2 \,z^2+8 \,z^4}{2 \,r^9}
\end{aligned}[/math]
We can repeat this process for higher-order terms and we should calculate that:
[math]\begin{aligned}
\Delta F_{4,x} &= -\frac{\partial \,\Delta u_4}{\partial x} = J_4\,\frac{15 \,x \,\left(x^4+2 \,x^2 \,\left(y^2-6\, z^2\right)+y^4-12 \,y^2 \,z^2+8 \,z^4\right)}{8 \,r^{11}} \\
\Delta F_{4,y} &= -\frac{\partial \,\Delta u_4}{\partial y} = J_4\,\frac{15 \,y \,\left(x^4+2 \,x^2\, \left(y^2-6 \,z^2\right)+y^4-12 \,y^2 \,z^2+8 \,z^4\right)}{8 \,r^{11}} \\
\Delta F_{4,z} &= -\frac{\partial \,\Delta u_4}{\partial z} = J_4\,\frac{5 \,z \,\left(15 \,x^4+10 \,x^2 \,\left(3 \,y^2-4 \,z^2\right)+15 \,y^4-40 \,y^2 \,z^2+8 \,z^4\right)}{8\,
r^{11}}
\end{aligned}[/math]
and:
[math]\begin{aligned}
\Delta F_{5,x} &= -\frac{\partial \,\Delta u_5}{\partial x} = J_5\,\frac{21 \,x \,z \,\left(5 \,x^4+10 \,x^2 \,\left(y^2-2 \,z^2\right)+5 \,y^4-20 \,y^2 \,z^2+8 \,z^4\right)}{8\,
r^{13}} \\
\Delta F_{5,y} &= -\frac{\partial \,\Delta u_5}{\partial y} = J_5\,\frac{21 \,y \,z \,\left(5 \,x^4+10 \,x^2\, \left(y^2-2 \,z^2\right)+5 \,y^4-20 \,y^2 \,z^2+8 \,z^4\right)}{8\,
r^{13}} \\
\Delta F_{5,z} &= -J_5\,\frac{3 \,\left(5 \,x^6+15 \,x^4 \,\left(y^2-6 \,z^2\right)+15\, x^2 \,\left(y^4-12\, y^2 \,z^2+8\,
z^4\right)+5 y^6-90 y^4 z^2+120 y^2 z^4-16 z^6\right)}{8 r^{13}}
\end{aligned}[/math]
I think these expansions are what you were looking for. If you have any questions, feel free to ask.
---------- Post added at 11:09 AM ---------- Previous post was at 08:15 AM ----------
I've cooked up a scheme for evaluating the zonal contributions to the Earth's gravitational acceleration. To do this efficiently, one ends to calculate the Legendre polynomials and their first derivatives using a recursive scheme. In Mathematica, this recursive scheme can be defined as follows:
This function takes a cartesian x-y-z coordinate in Earth's equatorial reference frame and calculates the x, y and z components of the gravitational acceleration due to the J2, J3, J4 and J5 components. This function is called using:
which sets up the J2, J3, J4, J5 values and for an [imath]x[/imath]-[imath]y[/imath]-[imath]z[/imath] coordinate [imath](3776163. ,\, 4500255.,\, 3370373.)[/imath] in metres. It returns the force components as:
[imath]F_{2,\,x} = 0.00166198[/imath] m s^-2
[imath]F_{2,\,y} = 0.00198067[/imath] m s^-2
[imath]F_{2,\,z} = -0.0109722[/imath] m s^-2
[imath]F_{3,\,x} = 0.0000162322[/imath] m s^-2
[imath]F_{3,\,y} = 0.0000193447[/imath] m s^-2
[imath]F_{3,\,z} = 0.0000210893[/imath] m s^-2
[imath]F_{4,\,x} = 0.0000138916[/imath] m s^-2
[imath]F_{4,\,y} = 0.0000165554[/imath] m s^-2
[imath]F_{4,\,z} = 0.0000053586[/imath] m s^-2
[imath]F_{5,\,x} = 0.0000003990[/imath] m s^-2
[imath]F_{5,\,y} = 0.0000004756[/imath] m s^-2
[imath]F_{5,\,z} = -0.0000026319[/imath] m s^-2
These values aren't exactly the same as those that you have calculated (because I'm using slightly different values for the coefficients) but they are close enough for comparison purposes.
If you need the recursive algorithm written in a more useful language such as C/C++, let me know.